MNIST手写数字识别（从零实现FFN）

本文是我的技术类第一篇文章，介绍如何在不依赖深度学习框架的情况下，仅使用 NumPy 从零实现一个用于 MNIST 手写数字分类的前馈神经网络（FFN）。本教程保留全部细节，以尽可能清晰的方式呈现深度学习模型的完整训练流程。

本文所有代码都置于个人github仓库点击跳转

0.序言

对于深度学习初学者来说，MNIST手写数字识别（以下用MINST简称）一定是一个绕不开的项目。作为最基础的项目，MNIST能教会初学者基础的：

完整的机器学习流程

神经网络的基本结构

张量思维

模型评估和调参

所以笔者认为掌握这个项目是至关重要的。

在本文中，笔者力求用最基础、简洁的语言，以及不省略任何细节的形式来完整讲述项目的全部流程。如果觉得啰嗦的话请快进哈哈

1.项目概览

1.1 MNIST是什么

MNIST 是一个手写数字图片数据集，主要用于识别 0–9 这十个数字。它最早由美国国家标准与技术研究院（NIST）制作，后由 Yann LeCun 等人清洗整理成 “Modified” 版本（MNIST）~~加入了M~~。

原始的 MNIST 数据通常是四个 .idx 文件，分别为：

train-images-idx3-ubyte：训练图像
train-labels-idx1-ubyte：训练标签
t10k-images-idx3-ubyte：测试图像
t10k-labels-idx1-ubyte：测试标签

数据集分为训练集+测试集，每一个集合里又有图像和对应的标签。训练集中一共有60000张，而测试集中一共有10000张图片。在数据集中图片是被打乱放置的，也就是说数据集中随机排列着0-9这十种数字。每张图片的大小为28*28像素，而每一个像素值的范围是0-255（从黑0到白255，灰度值）。

举个例子：数字7的数据是： [0,0,0,...,235,255,...,0,0,...,45,168,159,...,0,0]
他的标签就是：[7, 0, 4, 1, 9, 2, 1, 3, …]

1.2 目的

本项目旨在不利用任何深度学习框架，只用numpy来构建FFN（Feed-Forward Network）前馈神经网络来实现对MNIST数据集的手写数字分类。

用大白话来讲，就是让模型学会：给他一张图，他就能判断上面写的数字是几这个能力。

1.3 开发环境

本项目利用了如下四个库

numpy
gzip
struct
matplotlib

其中 gzip,struct是Python标准库所以不用下载，剩余的numpy和matplotlib的下载方式为：

1	pip install numpy matplotlib

1.4 数据集下载

数据集下载有三种方式：

到我的github仓库里下载点击跳转。最省事🤣
利用Python自带的库来下载

下载数据集

import urllib.request

urls = {
    "train-images": "https://storage.googleapis.com/cvdf-datasets/mnist/train-images-idx3-ubyte.gz",
    "train-labels": "https://storage.googleapis.com/cvdf-datasets/mnist/train-labels-idx1-ubyte.gz",
    "test-images":  "https://storage.googleapis.com/cvdf-datasets/mnist/t10k-images-idx3-ubyte.gz",
    "test-labels":  "https://storage.googleapis.com/cvdf-datasets/mnist/t10k-labels-idx1-ubyte.gz",
}

for name, url in urls.items():
    print("Downloading:", name)
    urllib.request.urlretrieve(url, f"{name}.gz")

print("Done!")

复制到vscode中可以直接使用
3. 使用pytorch下载（唯一用到pytorch的地方）

使用pytorch下载

from torchvision import datasets, transforms

mnist_train = datasets.MNIST(
    root='./data',
    train=True,
    download=True,
    transform=transforms.ToTensor()
)

mnist_test = datasets.MNIST(
    root='./data',
    train=False,
    download=True,
    transform=transforms.ToTensor()
)

注意:无论利用哪一种方法下载请务必注意文件路径!如使用本文的代码,请把数据集文件放置在./data/MNIST/raw下面.

MNIST/
│
├── data/MNIST/raw     
│ ├── train-images-idx3-ubyte(.gz)
│ ├── train-labels-idx1-ubyte(.gz)
│ ├── t10k-images-idx3-ubyte(.gz)
│ └── t10k-labels-idx1-ubyte(.gz)
└── main.ipynb(主程序文件)

2.模型代码

2.1 引入库

import numpy as np
import gzip
import struct
import matplotlib.pyplot as plt

这里简单讲一下四个库的用途：

numpy：把数据转换为矩阵；做矩阵相关的计算；初始化权重等。
gzip：打开 .gz 压缩文件；解压得到原始二进制数据；读取里面的 idx 格式内容
struct：解析二进制数据，把字节转换成整数/浮点数。
matplotlib：Python 的画图工具，负责可视化。

2.2 读取数据

首先定义读取数据和读取标签的函数。

def load_images(filename):
    with gzip.open(filename,'rb') as f:
        magic, num, rows, cols = struct.unpack('>IIII',f.read(16)) 
        data = np.frombuffer(f.read(),dtype=np.uint8)
        images = data.reshape(num,rows, cols)
    return images

def load_labels(filename):
    with gzip.open(filename,'rb')as f:
        magic, num = struct.unpack(">II",f.read(8))
        labels = np.frombuffer(f.read(),dtype=np.uint8)
        return labels

首先使用gzip来打开.gz压缩文件。使用f.read(16)来读取16个字节。
为什么是是16个字节呢？因为在标准MNIST图像文件中前十六个字节格式是：

0–3 magic number（文件类型，例如图像文件为2051，标签文件为2049）
4–7 num（图片数量）
8–11 rows（每张图的高度）
12–15 cols（宽度）

‘>IIII’ 是解析格式，一个I表示4字节无符号整数。所以四个I表示四个int(magic, num, rows, cols)。struct.unpack() 把二进制转换成 4 个整数。读取后存放至对应变量。在这一步，我们知道了一共有多少张图片（60000）、每张图片的行像素数（28）、列像素数（28）。
接下来用f.read()和np.frombuffer来读取所有图像像素，并把他们转换成Numpy数组。
最后用.reshape()来把一大长排的像素重塑成我们想要的形状，也就是(num, rows, cols)。转换之后，数据就变成了(60000, 28, 28)的MNIST标准格式（60000张图片，每个图片为28*28）。

接下来使用刚才定义的函数来读取数据：

1 2	train_images = load_images('./data/MNIST/raw/train-images-idx3-ubyte.gz') train_labels = load_labels('./data/MNIST/raw/train-labels-idx1-ubyte.gz')

2.3 数据预处理

为了使神经网络能够更快、更准确的学习到数据的规律，同时为了避免梯度爆炸和梯度消失，我们把所有像素数据除以255来实现归一化。

1	train_images = train_images.astype(np.float32)/255.0

因为神经网络输入层为784个神经元，所以需要把所有向量展平成(60000,784)的格式

title

1	train_images = train_images.reshape(train_images.shape[0],-1)

接下来给每一个图片制作one hot编码。

One hot
One hot编码，也叫独热编码是深度学习中给数据做标签的标准方式。
One-Hot 编码就是把一个“类别数字”变成一个“只有一个 1，其它都是 0 的向量”。例如标签是3的话，编码后就变成了[0,0,0,1,0,0,0,0,0,0]（因为第一个是0所以在第4位上）

def one_hot(labels, num_classes = 10):
    result = np.zeros((labels.size, num_classes))
    result[np.arange(labels.size),labels] = 1
    return result

train_labels_oh = one_hot(train_labels)

2.4 设定模型

2.4.1 初始化数据

本次我们的模型为输入784，中间层128，输出为10的FFN模型。

初始化数据

input_size = 784
hidden_size = 128
output_size = 10

np.random.seed(0)
W1 = np.random.randn(input_size, hidden_size) * 0.01
b1 = np.zeros((1, hidden_size))
W2 = np.random.randn(hidden_size, output_size) * 0.01
b2 = np.zeros((1, output_size))

2.4.2 激活函数

本次我们利用relu 和 softmax来进行对函数的激活

def relu(x):
    return np.maximum(0, x)


def softmax(x):
    exp_x = np.exp(x - np.max(x, axis=1, keepdims=True))
    return exp_x / np.sum(exp_x, axis=1, keepdims=True)

2.4.3 前向传播

接下来进行前向传播（Forward pass）。

前向传播的作用是根据输入x，计算神经网络的输出（预测结果）。

def forward(x):
    z1 = np.dot(x, W1) + b1
    a1 = relu(z1)
    z2 = np.dot(a1, W2) + b2
    a2 = softmax(z2)
    return z1, a1, z2, a2

输入层 (784)
   ↓
全连接层 W1 + b1
   ↓
ReLU 激活
   ↓
全连接层 W2 + b2
   ↓
Softmax（输出 10 类概率）

所以 forward() 的任务就是一层一层计算这些。

2.4.4 损失函数

接下来定义损失函数。本次利用交叉熵损失函数(cross-entropy loss)

交叉熵损失

交叉熵损失用来衡量“预测概率分布”和“真实分布”之间的差距。
也就是差距越小 → 模型越好。

$$
L = -\frac{1}{N} \sum_{i=1}^{N} \sum_{c=1}^{10} y_{i,c} \log \left( p_{i,c} \right)
$$
其中：

$y_{i,c}$ = One hot标签

$p_{i,c}$ = softmax输出的真实概率

def cross_entropy_loss(y_true, y_pred):
    eps = 1e-12
    y_pred = np.clip(y_pred, eps, 1. - eps)
    N = y_true.shape[0]
    return -np.sum(y_true * np.log(y_pred)) / N

其中eps = 1e-12和np.clip()的作用是通过设定一个最小值来防止log(0)输出无限而崩溃。

2.4.5 反向传播

def backward(x, y_true, z1, a1, z2, a2, lr=0.01):
    global W1, b1, W2, b2
    m = x.shape[0]

    dz2 = (a2 - y_true) / m
    dW2 = np.dot(a1.T, dz2)
    db2 = np.sum(dz2, axis=0, keepdims=True)

    da1 = np.dot(dz2, W2.T)
    dz1 = da1 * (z1 > 0)
    dW1 = np.dot(x.T, dz1)
    db1 = np.sum(dz1, axis=0, keepdims=True)

    W2 -= lr * dW2
    b2 -= lr * db2
    W1 -= lr * dW1
    b1 -= lr * db1

反向传播通过链式法则计算每个参数的梯度，包括：

输出层梯度：a2 - y
W2、b2 的梯度：来自 a1
隐藏层激活梯度：z1 > 0
W1、b1 的梯度：来自输入 x

这部分的原理详见另一篇文章（尚未更新）。

2.5 模型训练

epochs = 60
batch_size = 256
loss_history = []

for epoch in range(epochs):
    permutation = np.random.permutation(train_images.shape[0])
    X_shuffled = train_images[permutation]
    Y_shuffled = train_labels_oh[permutation]

    epoch_loss = 0
    batches = 0

    for i in range(0, X_shuffled.shape[0], batch_size):
        x_batch = X_shuffled[i:i + batch_size]
        y_batch = Y_shuffled[i:i + batch_size]

        z1, a1, z2, a2 = forward(x_batch)
        loss = cross_entropy_loss(y_batch, a2)
        backward(x_batch, y_batch, z1, a1, z2, a2)

        epoch_loss += loss
        batches += 1

    avg_loss = epoch_loss / batches
    loss_history.append(avg_loss)
    print(f"Epoch {epoch + 1:02d} | Loss: {avg_loss:.4f}")

其中：

epochs: 训练轮数（epoch = 60意味着把整个数据重复训练60回，遍历60000张图片60回）
batch_size: 每一批次放进模型的样本数(batch_size = 60意味着一股放进256个样本来进行前向传播和反向传播，60000/256 ≈ 234个batch)
np.random.permutation的作用是在每一个epoch中把训练数据随机排列。
接下来进行前向传播 -> 计算误差 -> 反向传播然后在每一次epoch结束后打印这个epoch的loss。

2.6 模型评估

在训练集上进行评估：

def accuracy(x, y_true):
    _, _, _, a2 = forward(x)
    y_pred = np.argmax(a2, axis=1)
    y_true_labels = np.argmax(y_true, axis=1)
    return np.mean(y_pred == y_true_labels)


print("Training Accuracy:", accuracy(train_images[:10000], train_labels_oh[:10000]))

这部分很简单，就是代入最后的参数，通过前向传播去得到输出概率。然后通过np.argmax来获得最大概率的数字下标。
y_pred == y_true_labels输出的是一组布尔值[True,False,True,...]而np.mean则会算出这个数组中True/all的值，也就是正确率。

2.7 损失曲线可视化

这一步我们要看到我们的损失曲线是如何下降的。

plt.plot(range(1, epochs + 1), loss_history, marker='o')
plt.title('Loss Curve (Training)')
plt.xlabel('Epoch')
plt.ylabel('Average Loss')
plt.grid(True)
plt.show()

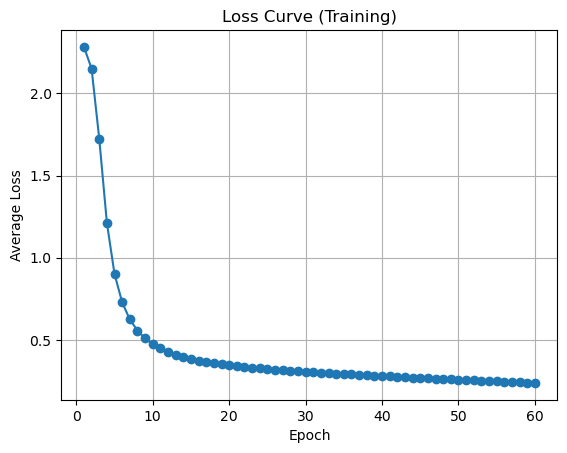
损失曲线

2.8 测试模型

最后我们要用之前准备的测试集去测试我们的模型

test_images = load_images('./data/MNIST/raw/t10k-images-idx3-ubyte.gz')
test_labels = load_labels('./data/MNIST/raw/t10k-labels-idx1-ubyte.gz')

test_images = test_images.astype(np.float32) / 255.0
test_images = test_images.reshape(test_images.shape[0], -1)
test_labels_oh = one_hot(test_labels)

test_acc = accuracy(test_images, test_labels_oh)
print(f"Test Accuracy: {test_acc * 100:.2f}%")

和之前一样去加载测试集，给测试集的数据做归一化和矩阵形状调整。使用之前计算好的最终参数代入accuracy()这个函数去计算正确率。

3.后记

至此MNIST手写数字识别这个项目的讲解就全部结束了。本项目的训练集和测试集正确率皆约为93%左右，如果在多加一个中间层，以及增多epoch的话也许可以提高到97%以上。

以上即为从零实现一个 MNIST FFN 模型的完整流程。如果你对反向传播原理或如何扩展网络结构感兴趣，我会在后续文章中继续展开。